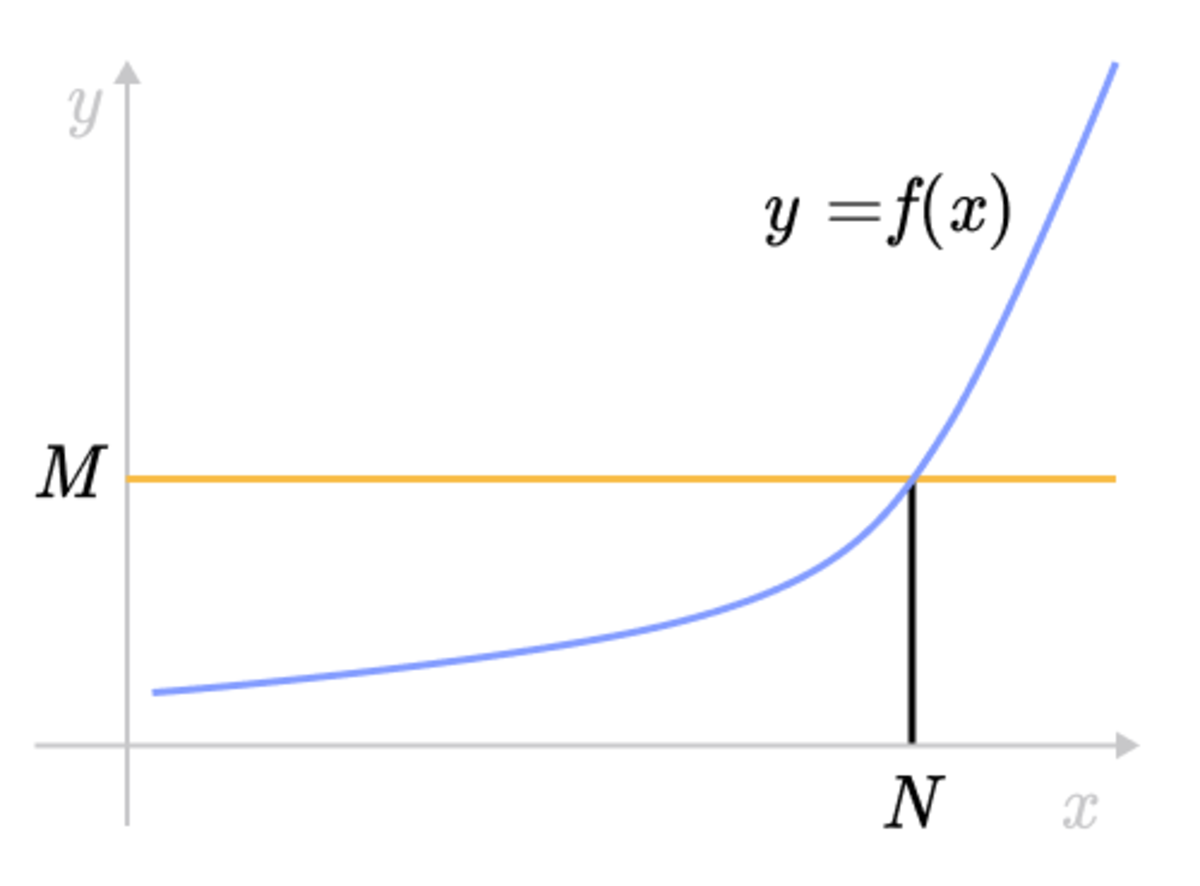
What is the difference between an equation written in function notation and one that is not?Definition for Y = f(X) Y=f(x) is a concept regarding the setup of a formula used to perform analysis during problemsolving efforts Let's look at how Y=F(x) works within the problemsolving process, the benefits of Y=F(x), as well as some frequently asked questionsAnd "( f o g)(x)" means "f (g(x))" That is, you plug something in for x , then you plug that value into g , simplify, and then plug the result into f The process here is just like what we saw on the previous page, except that now we will be using formulas to find values, rather than just reading the values from lists of points
E 3x On The Interval 0 3 Suppose That F X Chegg Com
F(x y z)=0 meaning
F(x y z)=0 meaning-The inverse f1 (x) = 3 sqrt(x5)/2 Start with x x;The Ftest of overall significance indicates whether your linear regression model provides a better fit to the data than a model that contains no independent variablesIn this post, I look at how the Ftest of overall significance fits in with other regression statistics, such as RsquaredRsquared tells you how well your model fits the data, and the Ftest is related to it



Calculus The Definition Of The Derivative
Subtract 5 2(x3) 25; Ex 131, 25 Evaluate lim┬(x→0) f(x), where f(x) = { (x/x@0,)┤, 8(x≠0@x=0) Finding limit at x = 0 LHL at x → 0 lim┬(x→0^− ) f(x) = lim┬(h→0) f(0F (x) is a function g from the reals to the reals, whose domain is the set of the reals x, such that f(x) ≠ 0 The range of a function is the set of the images of all elements in the domain However, range is sometimes used as a synonym of codomain, generally in old textbooks
If F(x)=x has no real solution then also F(F(x)=x has no real solutionAnswers Click here to see ALL problems on Graphs Question 4173 what does g (x) and f (x) mean and what purpose do they serve?As it stands, the function can't be defined at $0$, since the top and bottom both evaluate to $0$, and $0/0$ isn't defined If, instead, you define $f$ as $$ f(x)=\begin{cases}\frac1N\frac{1e^{2\pi ix}}{1e^{2\pi ix/N}}&x\neq 0\\5em \phantom{\frac1N1}1&x=0\end{cases} $$
Divide by 2 (x5)/2A function may be thought of as a rule which takes each member x of a set and assigns, or maps it to the same value y known at its image x → Function → y A letter such as f, g or h is often used to stand for a functionThe Function which squares a number and adds on a 3, can be written as f(x) = x 2 5The same notion may also be used to show how a function affects particular valuesThe first one gives critical values of F at the p = 005 level of significance The second table gives critical values of F at the p = 001 level of significance 1 Obtain your Fratio This has (x,y) degrees of freedom associated with it 2 Go along x columns, and down y rows The point of intersection is your critical Fratio 3



Solution It Says Quot Find F X 0 Quot What Does It Mean The Porblem F X 3x 12



2
The expression "f (x)" means "a formula, named f, has x as its input variable" It does not mean "multiply f and x "!Divide by 5 (x2) / 5 ;\Fourier sine series" Computing coe cients in an orthogonal expansion is just a matter of taking inner products B n =



Faculty Math Illinois Edu Pat Fa07 Lab Pracmast2sol Pdf
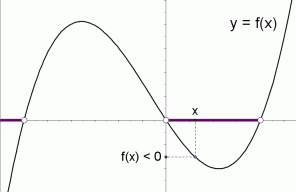



Graphical Interpretation Of Sentences Like F X 0 And F X 0
Since we're looking for f (x)=0, we're looking for y=0 since y and f (x) can be interchanged In other words, we are looking for the xintercept, since y=0 for all xintercepts So we substitute 0 in for f (x) and we get Now we solve for xThe f is because there's no need for the operation to be done in double I expect there's more chance of an implementation where 10/i would be significantly slower for no benefit (software float emulation, indifferent optimization), than one where 10f is significantly slower for no benefit (if double is faster than float that's because you have fp hardware, so conversion between the twoA) If f'(x) >0 on an interval, then f is increasing on that interval b) If f'(x) 0 on an interval, then f is concave upward on that interval d) If f''(x)




Example 15 F X 1 X What Is The Domain And Range Examples



What Is Calculus
Let f ''(x) = 4x3 2x and let f(x) have critical numbers 1, 0 and 1 Use the Second Derivative Test to determine which critical numbers, if any, give a relative maximumNow the function values in the f(x) table are all one lower than the corresponding values in the table for g(x) = x 2 and the graph has moved down by one unit Notice that in this example the graph of f(x) = x 2 − 1 crosses the x – axis in two places This means that the equation x 2 − 1 = 0 has two solutions, x 2 − 1 = 0 x 2 = 1 x = ± 1 which are x = −1 and x = 1Increasing/Decreasing Test If f′(x) > 0 for all x ∈(a,b), then f is increasing on (a,b) If f′(x) < 0 for all x ∈(a,b), then f is decreasing on (a,b) First derivative test Suppose c is a critical number of a continuous function f, then Defn f is concave down if the graph of f




Limits
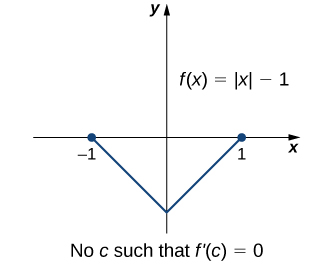



3 4 The Mean Value Theorem Mathematics Libretexts
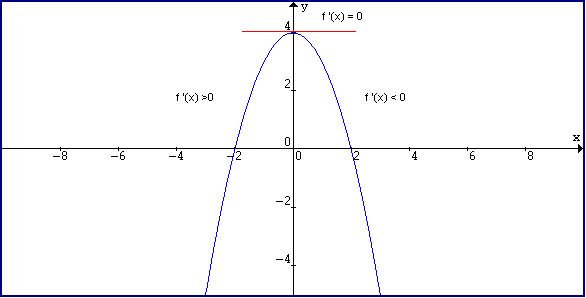
17 0 5e7 0 01 02 03 04 05 06 07 08 09 1 17 © Urban Dictionary ® advertise • terms of serviceIf we use,,y=2x,,,this is well defined, on a xy coordinate plane, y rises twice as fast as x moves to rightHow To Tell Where f (x) is Less Than 0 or Greater Than 0




If F X Satisfies The Requirements Of Lagrange S Mean Value Theorem On 0 2 And If F 0 0 An Youtube



Limit Definition Of A Derivative
Don't embarrass yourself by pronouncing (or thinking of) " f ( x ) " as being " f times x ", and never try to "multiply" the function name with its parenthesised inputIt is a different way of writing "y" in equations, but it's much more useful!Multiply by 2 2(x3) 2;




Verify Lagrange S Mean Value Theorem For The Following Functions In The Given Intervals F X Youtube




Derivative Of Exponential Function What Does This Text Mean Mathematics Stack Exchange
If f 0, 1 → 0, 0) is differentiable function with decreasing first derivative, such that f(0) = 0 and f'(x) > 0 then 1 dx tan'f(1) Statement 1 bra f'(x)1 f'(1) 0 dx Statement 2 S f(1) f'(1) f(x)1 (A) Both the statements are true and statement 1 is the correct explanation of statement 2 (B) Both the statements are true and statement 1 is not the correct explanation of statement 2 Be very careful with this fact It DOES NOT say that if \(W(f,g)(x) = 0\) then \(f(x)\) and \(g(x)\) are linearly dependent!Answer to What does f(x) = 2 mean?




One To One Functions And Their Inverses Ck 12 Foundation




The Definition Of The Derivative Wolfram Demonstrations Project
Answer by RAY100 (1637) ( Show Source ) You can put this solution on YOUR website!If X>03, then you areCritical Points Definition of a critical point a critical point on f (x) occurs at x 0 if and only if either f ' (x 0) is zero or the derivative doesn't exist Extrema (Maxima and Minima) Local (Relative) Extrema Definition of a local maxima A function f (x) has a local maximum at x 0 if and only if there exists some interval I containing x



Www Math Cuhk Edu Hk Course Builder 1718 Math1010j 1010lect14 Pdf



Graphs Of Functions
F(x) means that we have a function of x The zero of the function f(x)=2x2 is the xvalue that makes f(x) = 0 So we can just set the function equal to 0, and then solve for x!Y = f (x) Process Outcome a Result of Process Inputs The mathematical term Y = f (x), which translates as simply " Y is a function of x," illustrates the idea that the important process outcomes ( Y s) are a result of the drivers ( x 's) within processes The goal of DMAIC is to identify which few process and input variables mainlySo f (x) shows us the function is called " f ", and " x " goes in And we usually see what a function does with the input f (x) = x2 shows us that function " f " takes " x " and squares it Example with f (x) = x2 an input of 4 becomes an output of 16 In fact we can write f (4) = 16
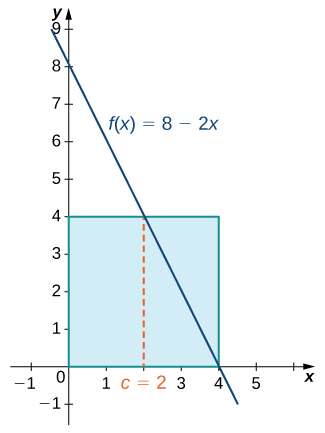



5 3 The Fundamental Theorem Of Calculus Calculus Volume 1




Taylor Series Wikipedia
By signing up, you'll get thousands of stepbystep solutions to your homework questions You can also ask yourThe inverse f1 (x) = (x2)/5 Start with x x ; We want the values of x that give a y value greater than 0 Let's say that f(x)=x^210 The graph below shows y=f(x) graph{x^210 6, 6, 15, 15} When we want f(x)>0, we want y>0, or all the values of x where f(x)>0 In this instance, x^210>0 x^2>10 x>sqrt(10) x




Let For Function F X Cos 1 X 1 Le X Le 0 Mx




Justification With The Mean Value Theorem Table Video Khan Academy
Decide whether $f(x)=x$ is bounded above or below on the interval $0,a$ where $a$ is arbitrary, and whether the function takes on it's maximum or minimum value within that same interval This question is very straightforward, assuming $x=x$ But if that is the case, then the choice of notation is very strangeIn fact, it is possible for two linearly independent functions to have a zero Wronskian!Yeah, f (x) is the normal function, f' (x) is the first differential and f'' (x) is the second differential, ad infinitum




Slope X Intercept Y Intercept Meaning In Context Video Khan Academy



Inflection Points
F(x) = ˆ cx4 0 02, then you are succesful in round 2;Clearly, h(x) = (mx b)(nx c) is a polynomial of degree 2 and h(x) has two roots The respective roots are when f(x) = 0 and g(x) = 0 This means the graph of h(x) crosses the xaxis at the same two points as f(x) and g(x) Thus, if there are points of tangency then they must occur at these common points on the xaxis0 f(x)sin(nx dx R ˇ 0 sin 2( )dx = 2 Big payo completeness of eigenfunctions means that any smooth function with f(0) = 0 = f(ˇ) can be written f(x) = X1 n=1 B n sin(nx);



Find The Mean And Variance Of The Distribution F X 3e 3x 0 X 0 Elsewhere Sarthaks Econnect Largest Online Education Community



Http Cneacs Weebly Com Uploads 2 4 8 5 2 Sec 4 2 Mean Value Theorem Pdf
F (x) basically means y, and f' (x) means dy/dx The x can have a value, so for example, f (x) = 2x 1, then f (1) = 3 that is as good as I can explain it!!!By $f(x) = x^2 4$ I am telling you that if you input a number $x$ to this function then the function squares $x,$ subtracts 4 and returns the result Thus for example if $x = 3$ then $y = f(3) = 3^2 4 = 9 4 = 5$ To graph this function I would start by choosing some values of $x$ and since I get to choose I would select values that make the arithmetic easy X the inputs, factors or whatever is necessary to get the outcome (there can be more than one possible x) F the function or process that will take the inputs and make them into the desired outcome Simply put, the Y=f(x) equation calculates the dependent output of a process given different inputs



Increasing And Decreasing Functions




Property Of The Little O Notation In Calculus Apostol Mathematics Stack Exchange
Example 2 The function f(x) = 2(x3) 25, x≥3 Note that there is a restriction on x Start with x x; The derivative, f'(x), can be interpreted as "the slope of the tangent line" f'(x)> 0 means all tangent lines have positive slope are going up to the right Also "if x> 0, then f'(x)< 90" so for x positive, the derivative is negative which means tangent lines are going down to the rightThe ' (x)' is somewhat meaningless to the notation, and serves only to remind you what the independent variable is Say you have the function f (x)=x If you prefer variables like t, or s, for example the result of the function is the same That is, f (t)=t gives the same result as f (x)=x, when x



Calc 1 F X 0 If X 0 What Does This Mean Physics Forums




Big O Notation Wikipedia
Summary "Function Composition" is applying one function to the results of another (g º f) (x) = g (f (x)), first apply f (), then apply g () We must also respect the domain of the first function Some functions can be decomposed into two (or more) simpler functionsAdd 2 x2 ;$ f(x) $ är alltså en formel som beskriver funktionen, dvs sambandet mellan x och y Nyttan med denna är framförallt allt att det blir mycket tydligare hur man räknar ut funktionens värde
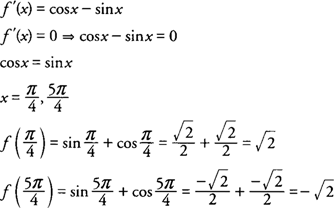



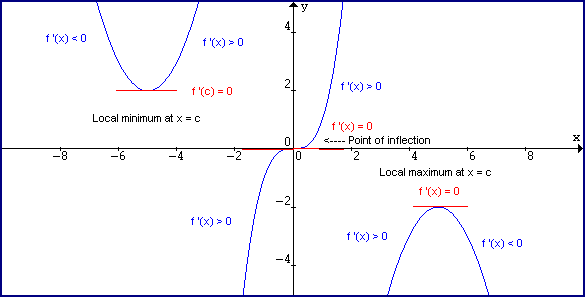
Critical Points



Http Www Columbia Edu Md3405 Maths D 14 Pdf
This fact is used to quickly identify linearly independent functions and functions that are liable to be linearly dependent How do you find the value of #f(9)# for #f(x)=x^22#? f (x,y) is function in x and y If you draw this in R 3, the function will lie in the xyplane The domain of the function is the xy plane or some subset of it The graph of the function is the ordered triples (x, y, z) for which z = f (x, y) Example z = ln (xy) The domain is the portion of the plane for which xy > 0, which is the interior




Verify Lagranges S Mean Value Theorem For The Following Function F X X 4 X 6 X 8 On 4 10



Activation Functions Fundamentals Of Deep Learning
Show more Tbh thats about as good as most people would be able to do and i didnt know that f' (x) was dy/dx 0What does a dependent and independent variable mean?




Lesson 19 The Mean Value Theorem Slides



World Web Math Derivatives Of Polynomials
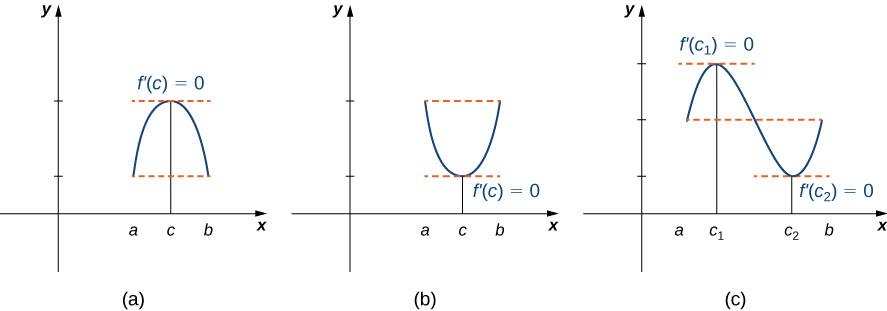



3 4 The Mean Value Theorem Mathematics Libretexts



Mi Schoolwires Net Cms Lib Mi Centricity Domain 429 Practice test 1 dsm part 1b my answer key Pdf



Local Extrema Of Functions



What Is The Difference Between F X 0 And F X 0 Quora



1



1
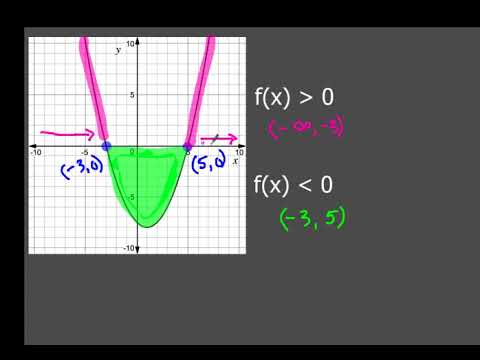



How To Tell Where F X Is Less Than 0 Or Greater Than 0 Youtube



Artofproblemsolving Com Downloads Printable Post Collections



What Does F 0 Represent On The Graph Of F X Quora




Derivative Wikipedia



Http Maths Dur Ac Uk Dma0wjz B1 Anlec1 Pdf



Users Math Msu Edu Users Magyarp Math132 Notes 3 2 Mean Value Theorem Pdf
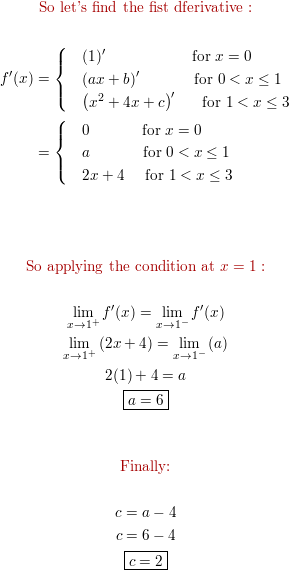



Determine The Values A B And C Such That The Function F Satisfies The Hypotheses Of The Mean Value Theorem On The Interval 0 3 F X 1 X 0 Ax B
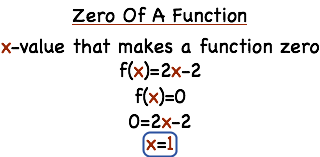



What S The Zero Of A Function Printable Summary Virtual Nerd
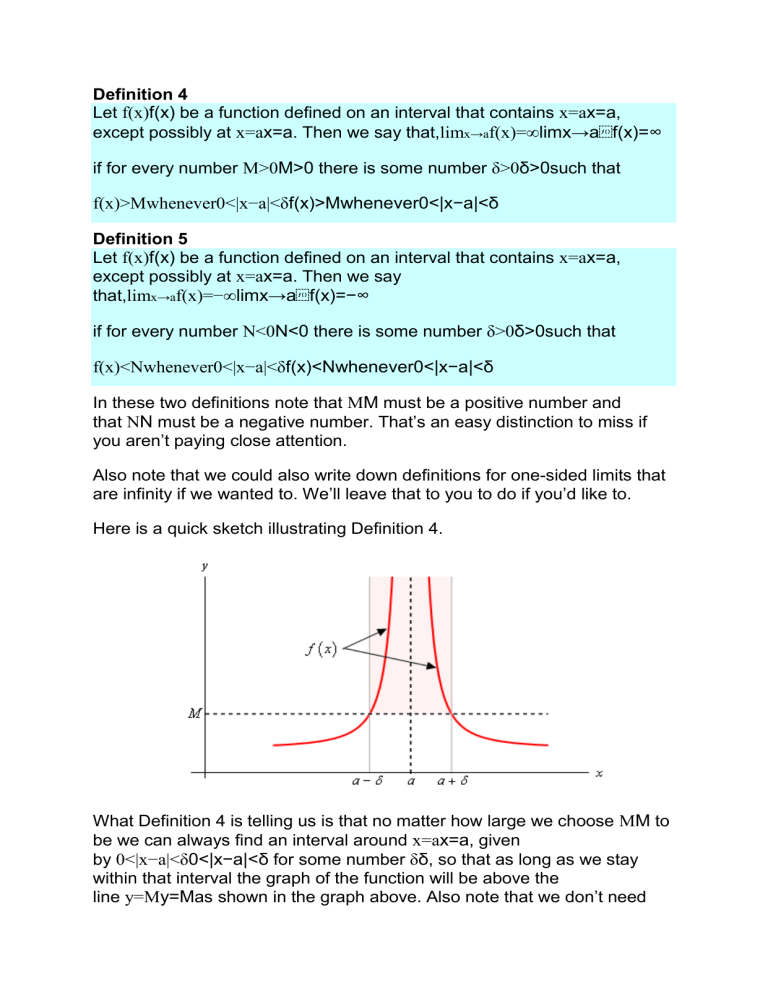



Definition 4




2 Recall That The Definition Of A Function F X Chegg Com
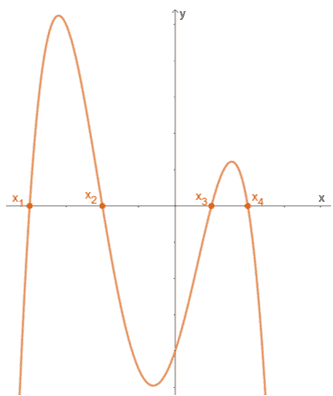



Zeros Of A Function Explanation And Examples



Calculus The Definition Of The Derivative
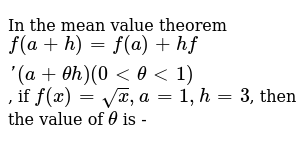



In The Mean Value Theorem F A H F A Hf A Theta H 0 Lt Th



Derivative And Tangent Line



Www Shsu Edu Kws006 Precalculus 1 1 Function Definition Files Ws Soln 1 1a Functiondefinition Pdf




Meaning Of The Notation Mathcal F X F X Mathematics Stack Exchange




What Is The Difference Between Y F X And Y F X Quora



Www Math Colostate Edu Clayton Teaching M113f10 Homework Hw9solutions Pdf




Does The Function Satisfy The Mean Value Theorem F X X 3 X 1 0 2 Find Numbers C Satisfy Youtube



Math Mychamplain Ca Files Cal1 Notes On Rolle Mvt Pdf



Www hs Boone K12 Ky Us Userfiles 531 Classes 9731 Quiz key Pdf Id




Answered 15 F X Vx 0 4 16 F X X Bartleby



Does Limit X 0 1 X Exist Quora



1




Ex 5 8 5 Verify Mean Value Theorem F X X3 5x2 3x
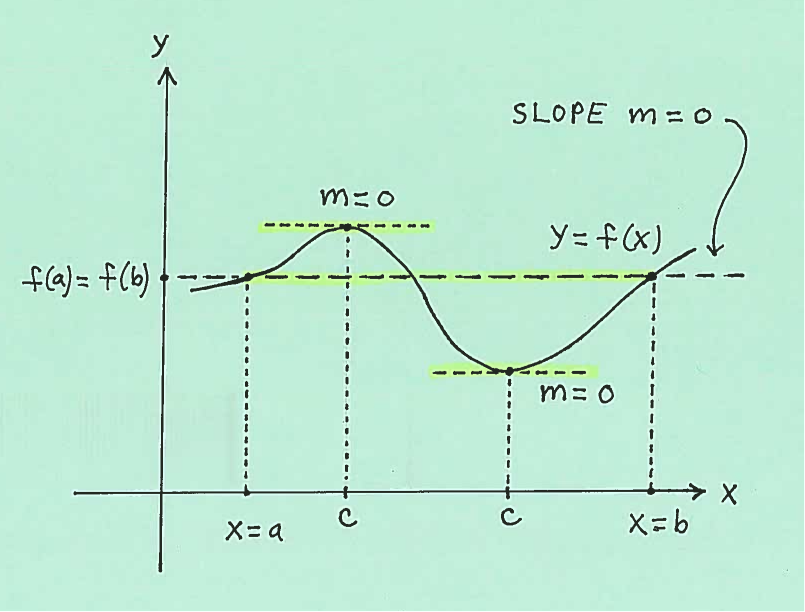



Mean Value Theorem Problems
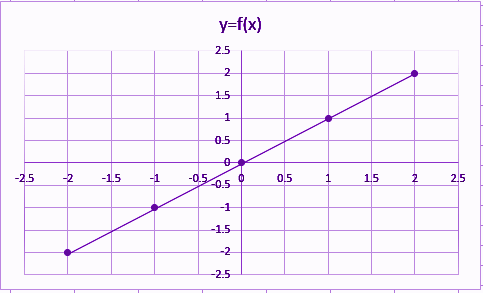



Identity Function Definition Graph Examples




Answered Find The Derivative Of The Function Bartleby



Interval Notation



Www Southhadleyschools Org Cms Lib Ma Centricity Domain 11 Theorems Pdf




I Didn T Understand The Below From Sets And Functions Algebra Caltech Pdf The Highlight Is My Problem What Does It Mean And Why Does Say X 0 Mathematics Stack Exchange
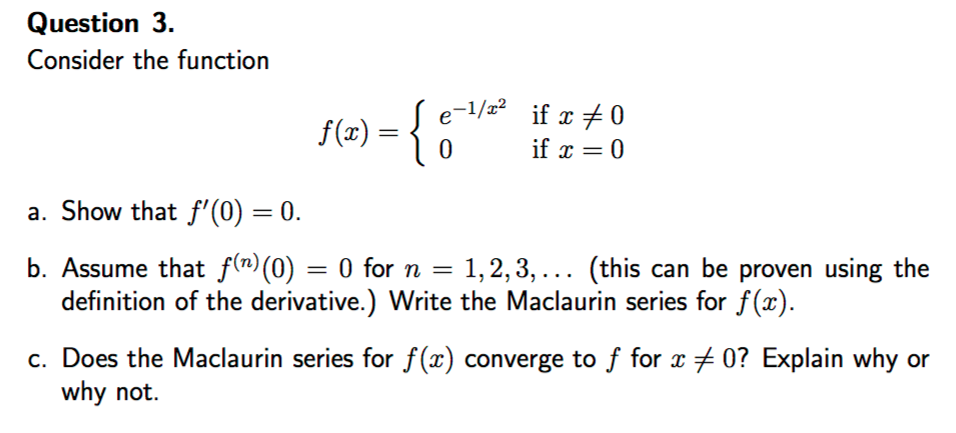



Consider The Function F X E 1 X 2 If X 0 0 If Chegg Com




Definition Of A Logarithmic Function For X 0 And B 0 B 1 Y Log B X Is Equivalent To B Y X The Function F X Log B X Is The Logarithmic Function Ppt Download



Help Online Quick Help Faq 871 Does Origin Have A If Function



2




If F X 0 At Each Point X Of An Open Interval A Chegg Com




Extrema Of A Function
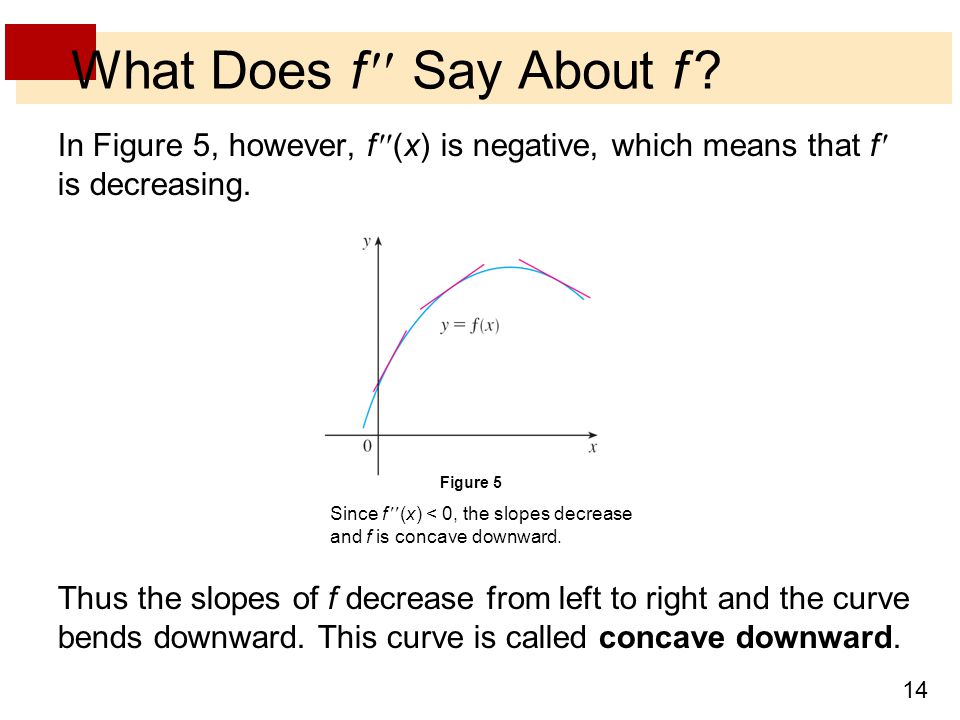



Limits And Derivatives Ppt Download
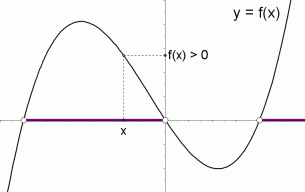



Graphical Interpretation Of Sentences Like F X 0 And F X 0



Epsilon Delta Definition Of A Limit Brilliant Math Science Wiki
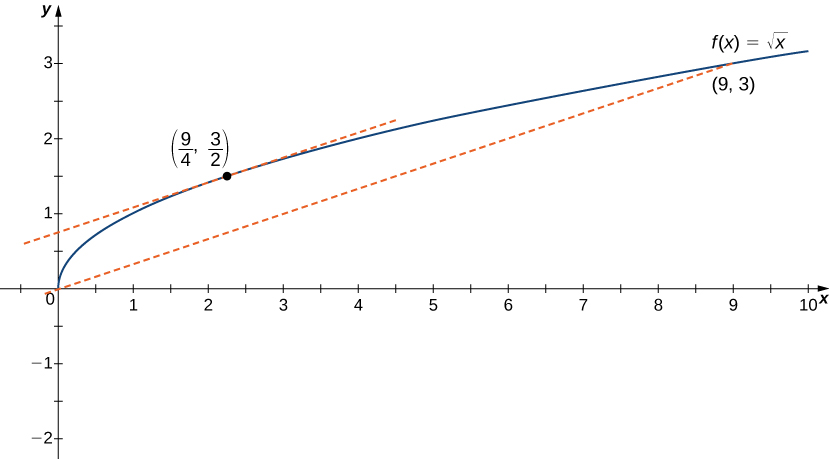



4 4 The Mean Value Theorem Calculus Volume 1
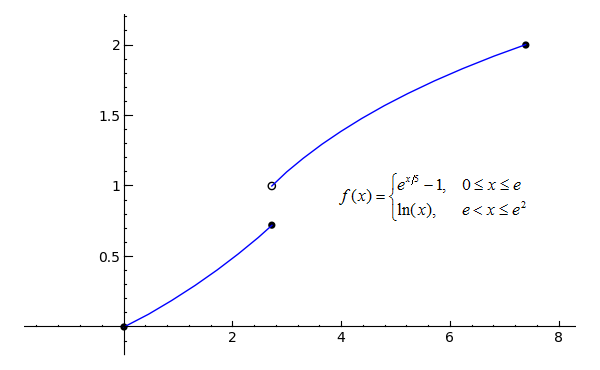



Sage Calculus Tutorial Continuity



Derivative And Tangent Line




The Function F X X 0 Lessthanorequalto X 1 0 Chegg Com




E 3x On The Interval 0 3 Suppose That F X Chegg Com




Let F X Be Defined In 0 1 Then The Domain Of Definition Of F E X F Ln X Is A 1 E 1 B E 1 C 1 E D E 2 E 2 2



Www Hoodriver K12 Or Us Cms Lib Or Centricity Domain 230 Uch 1 the derivative pt answer key Pdf
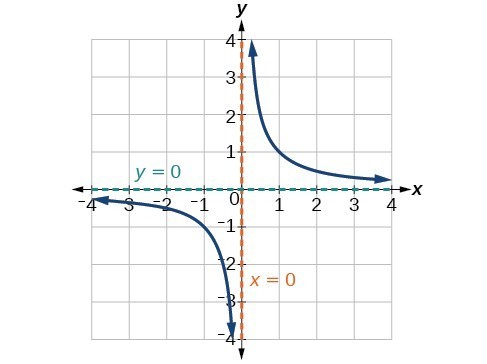



Use Arrow Notation College Algebra




Answered 8 For The Function F X 3x2 4x 1 Bartleby



Www3 Nd Edu Apilking Math Lectures 16 mean value theorem Pdf




1 Introduction To Limits
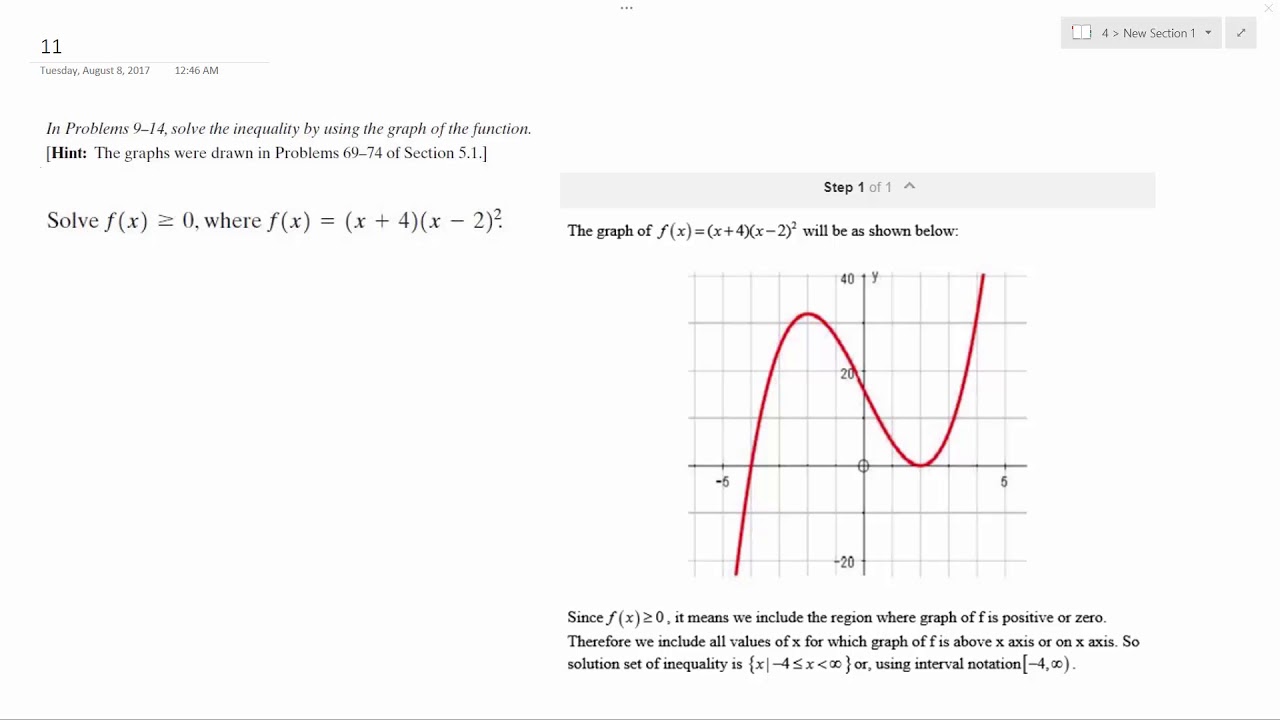



Solve F X Greater Than 0 Where F X X 4 X 2 2 Youtube




Rd Sharma Solutions Class 12 Chapter 15 Mean Value Theorems



Critical Points




The Joint Probability Density Function Is F X Y For 17 Find The Mean Of X Given Homeworklib




Problem 2 Find O Satisfying The Mean Value Theorem For F X On The Interval 0 1 Homeworklib




9 F X X4 8x On 0 2 Determine Whether The Mean Chegg Com




Question Video The Mean Value Theorem Nagwa



Www Jstor Org Stable



Continuity Of Functions



2




The Derivative



Users Math Msu Edu Users Wenbinli Math132 Ss16 Slides 3 2 Mean Value Theorem Pdf




Verify Mean Value Theorem For The Function F X X 3 5x 2 3x In The Interval A B Where A 1 And B 3 Find All Cepsilon 1 3 For Which F 1 C 0



0 件のコメント:
コメントを投稿